>>> előző rész folytatása >>>
A krátersűrűség-számítás módszere
Az égitestek történetének megismerésében felszínük különböző területeinek kora jelentős szerepet játszik, mert sok mindent elárulhat. A bolygófelszínek területeinek kormeghatározása, egymáshoz való viszonyítása és időbeli megfeleltetése, egymással való egyeztetése (korrelálása) nem véletlenül a planetológia egyik nagy kihívása.
A Naprendszer előzőekben felvázolt keletkezési modellje általános szabályként sugallja, hogy a kráterek minél nagyobbak annál idősebbek, és azt is, hogy az újabb időkben csak viszonylag kevés kráter keletkezik. Ugyanakkor, statisztikai alapon kijelenthető, hogy újabban a nagyobb testek ritkábban csapódnak be, mint a kisebbek. Mindezek alapján lehetségessé válhat a felszíni területek kráteres, viszonylagos kormeghatározása.
A kráterpopulációk kimutatása önmagában csak relatív összehasonlításokra alkalmas, noha a korrelálásnak kétségtelenül hasznos megoldási eszköze. Gyakorlatilag, így azt lehet megállapítani, hogy az égitestek felszínein bizonyos területek azonos, vagy különböző korúak, de azt, hogy maguk a korok hány évet jelentenek, csak feltételezni lehet.
A kráterpopulációk korát akkor lehet (lehetne) években meghatározni, ha az azokat alkotó kráterek korára vonatkozóan pontos kormeghatározási adatok állnak (állnának) rendelkezésre, és a különböző korok becsapódásainak gyakoriságára vonatkozó adatokat sikerül (sikerülne) megfelelően kiértékelni.
Földi viszonylatban a kráterek korát illetően a helyzet jónak mondható, és a holdi kőzetek laboratóriumi vizsgálatának köszönhetően már a Hold esetében sem rossz, így az abszolút (radiometrikus) kormeghatározás segítségével a relatív korrelációkhoz abszolút korok is kapcsolhatók. Ezek a módszerek azonban más égitestek eseteiben, legalábbis egyelőre, nem alkalmazhatók. Ezekben az esetekben kormeghatározásra most még csak a többi létező ismeretet lehet használni – leginkább a felszín legfelső rétegét mutató fényképfelvételeket.
Mivel közvetlen módszerekkel a becsapódások gyakoriságát mindenekelőtt az észlelések száma lenne hivatott megadni, ám az ilyenek jóformán csak becslések, a becsapódás-gyakoriság elfogadható megállapítására kidolgoztak egy közvetett módszert, éspedig a krátersűrűség kiszámolását. Ennek alapját a kráter-számlálási adatok képezik, amelyek viszont egyre pontosabbak, hiszen a kráterek számlálása a Föld felszínén rendszerint közvetlenül is elvégezhető, a felszín alatti különböző korú rétegekben lévő becsapódásos szerkezetek vizsgálatára pedig egyre jobb műszeres módszereket fejlesztenek ki. Sőt mi több, az űrből készített fényképek feldolgozása alapján, a krátersűrűség ma már a Naprendszer többi tagja esetében is kiszámolható1.
Kráterszámlálási adatok
A krátersűrűség meghatározásával tehát kideríthető az égitestek különböző területeinek egymáshoz viszonyított kora. A statisztikai adatok feldolgozását és kiértékelését grafikai megjelenítések segíthetik. Ilyen grafikus megjelenítés a differenciált méret-gyakoriság eloszlás, amelyet általában logaritmikus skálán ábrázolnak, illetve ennek egy változata, a relatív méret-gyakoriság eloszlás. Ezek feldolgozását és kiértékelését bízzuk azokra a szakemberekre, akik kimondottan ezzel foglalkoznak.
Az adatok azt mutatják, hogy az idős felszínek régóta inaktív területeit, például ahol nincs vulkánosság, több kráter borította be az idők során, mint a fiatalabbakat. Azokon a területeken, ahol a felszín valami miatt gyakorlatilag teljesen átalakult vagy újraképződött, a korábbi felszín becsapódásos kráterei eltűntek. Ezért ott csak kevesebb kráter látható, annyi, amennyi a legutolsó, a felszíni képződményeket eltörlő esemény – például erózió, vulkáni lávatakaró, beolvadás, tektonika, szubdukció – óta keletkezett. A felszínek régóta változatlan területei azonban egy idő után „betelnek”, azaz újabb kráter már csak úgy keletkezhet, ha a lövedék egy korábbi kráterbe csapódik. Annak megállapítása, hogy egy bizonyos terület valóban telítetté vált, illetve milyen régen került egyensúlyba, meglehetősen nehéz feladat. Mindezek ellenére, kráterszámlálás alapján általánosan elfogadott tényleges megállapítások is születtek, például azoknak a Jupiter-holdaknak az esetében, amelyeket még Galilei fedezett fel 1610-ben.
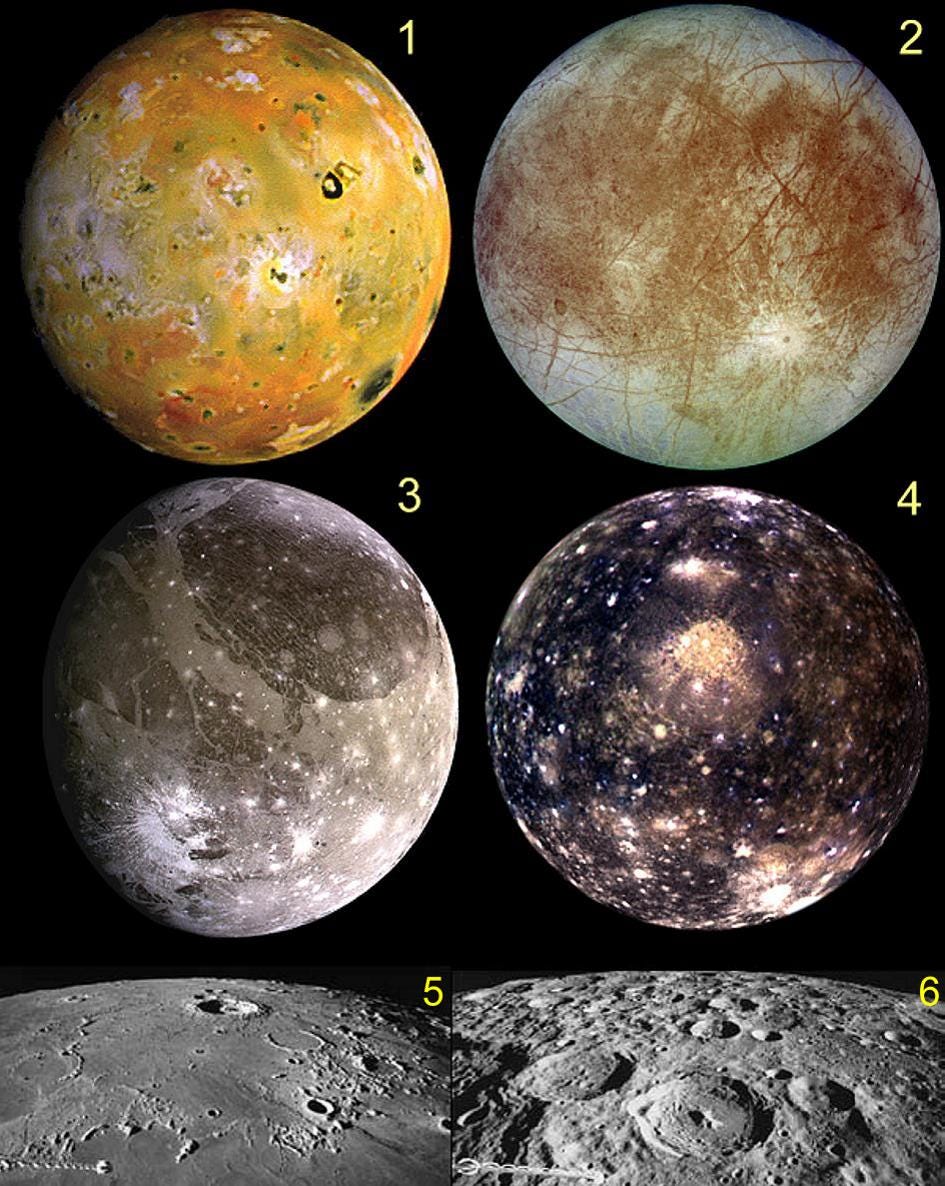
A Naprendszerben a legfiatalabb – 1 millió évesnél nem idősebb – felszínnel az Ió rendelkezik. Ennek a különleges holdnak a felszínén jelenleg nincsenek becsapódásos kráterek, vulkáni kalderából viszont sok van, ezért lehetséges, hogy az égitest éppen katasztrofális felszín-újraképződési szakaszban van. Ezt a felszínt hatalmas árapály- és elektromos erők alakítják. A vulkanikus működés olyan gyorsan újraburkolja, hogy a hold létrejötte óta akár sokszor is megismétlődhettek a felszínképződés folyamatai.
Az Europa hold jégtakaróval borított, sima felszíne fiatal és hamar megújuló, így csak kevés krátert találtak rajta. Közöttük azonban egészen különlegesek is vannak. Az Europán található Tyre macula egy kerekded, környezeténél világosabb, domborzatát teljesen elvesztett, nagy méretű becsapódásos szerkezet, mondhatni egy domborzat nélküli palimpszeszt, amelyet számos, sötét színű gyűrű határol.
A Ganimédesz barázdált felszínén a kráterek száma helyről helyre változik, ezáltal jelezve az egymáshoz közeli területek különböző korát. Felszínén két tájegység található. Az egyik, ahol sok a kráter, sötét, főleg szennyezett jégből álló ősi területekből áll. A másik, amely világos, valószínűleg olyan jégből áll, amely megolvadt, majd újabb lehűlését megelőzően az idősebb területekre ömlött. A kráterek a kőzet-jégholdakra jellemzően gödör- vagy dómközpontúak, kiemelt sánccal, befelé lejtő felszínű sáncfallal, néha teraszokkal.
A Callisto, amelyen már régóta megszűntek a vulkanikus és tektonikus folyamatok, nem csak a Jupiter rendszerében a kráterekkel legsűrűbben borított égitest, de egyben a Naprendszer legkráteresebb felszíne is. A legnagyobb becsapódás, amely érte, kialakította a Valhalla többgyűrűs medencét. A 4000 km széles gyűrűrendszer húsznál is több koncentrikus gyűrűgerince több nagy gyűrűhullámhoz tartozik, ez pedig vékony litoszférára és folyós asztenoszférára utal.
A Naprendszerben sokkal több a kis égitest, mint a nagy, így érthető, hogy kis kráterből sokkal több van, mint nagyból. A légkör nélküli égitesteket rengeteg mikrometeor is bombázza, számlálhatatlanul sok apró krátert hozva létre. Ezek porhanyósították a Hold felszínét, elősegítvén a holdpor megjelenését. A Föld légköre viszont természetes pajzsot alkot a mikrometeorok ellen, így ezek nem jelentenek gyakorlati veszélyt. A nagy becsapódások számításai azonban elgondolkodtató eredményeket adnak: 10 km átmérőjű kráterből egymillió év alatt csak egy keletkezik, de 1 km átmérőjűből már 5–10, 100 m átmérőjűből pedig mintegy 100. 100 m átmérőjű krátert létrehozó becsapódásra tehát nagyjából minden 10000 évben lehet számítani, ami földtörténeti szempontból nagyon rövid idő. Kisebb becsapódások pedig akár minden évezredben, évszázadban előfordulhatnak. A kráterszámlálási adatok egyre fontosabbá válnak a többi égitest felszín-történetének megismerésében is. A következő felsorolás néhány jellegzetes példát tartalmaz.
>>> folytatása következik >>>
Dorombi meséi
Történet, tudományos ismeretterjesztés, világkép.
• „Csillagos mesék” – igaz történetek, tudományos-ismeretterjesztő írások, a világról alkotott személyes meglátások.
• „Alternatív fikciók” – különleges történetek, amelyek a valóságból kiindulva többé-kevésbé az írói képzelet termékei.
• „Közérdekű vélemények” – olvasói írások, kommentek, igényes tartalmi és erkölcsi kivitelben.
Tartalmas kikapcsolódás, művelődés, kellemes időtöltés.
A krátersűrűség egy szám, amely kifejezi egy négyzetkilométer területen lévő kráterek számát, vagyis: kráterek száma / km2. Mivel azonban ritkán fordul elő, hogy egy bizonyos négyzetkilométeren pontosan meg lehessen számlálni a krátereket, a gyakorlatban kézenfekvő S = K/T képletet használni, ahol S = a tanulmányozott teljes terület kiszámolandó krátersűrűsége, K = a területen lévő kráterek száma, T = a terület mérete négyzetkilométerben megadva. Például, ha egy 152 km2 területet tanulmányozunk és azon 6 krátert számlálunk, akkor a krátersűrűség erre a területre S = 6/152 = 0,048.